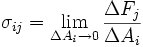
物体由于外因（受力、湿度、温度场变化等）而变形时，在物体内各部分之间产生相互作用的内力，以抵抗这种外因的作用，并试图使物体从变形后的位置恢复到变形前的位置。
在所考察的截面某一点单位面积上的内力称为应力。同截面垂直的称为正应力或法向应力，同截面相切的称为剪应力或切应力。

 

应力状态
物体由于外因（受力、湿度、温度场变化等）而变形时，在物体内各部分之间产生相互作用的内力，单位面积上的内力称为应力。应力是一个矢量，沿截面法向的分量称为正应力，沿切向的分量称为切应力
物体中一点在所有可能方向上的应力称为该点的应力状态。但过一点可作无数个平面，是否要用无数个平面上的应力才能描述点的应力状态呢？通过下面的分析可知，只需用过一点的任意一组相互垂直的三个平面上的应力就可代表点的应力状态，而其它截面上的应力都可用这组应力及其与需考察的截面的方位关系来表示。

 

 

应力张量

 

应力张量

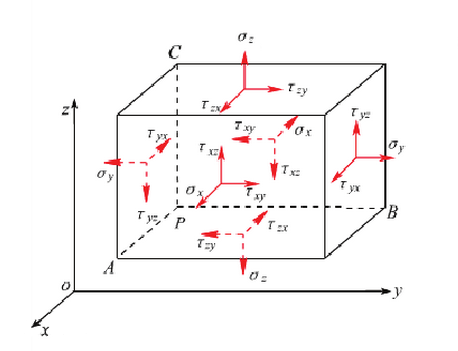
如图所示，P为直角坐标系0XYZ中一变形体内的任意点，在此点附近切取一个各平面都平行于坐标平面的六面体。此六面体上三个互相垂直的三个平面上的应力分量即可表示该点的应力状态。
为规定应力分量的正负号，首先假设：法向与坐标轴正向一致的面为正面；与坐 标轴负向一致的面为负面。进而规定：正面上指向坐标轴正向的应力为正，反之为负； 负面上指向坐标轴负向的应力为正，反之为负。三个正面上共有九个应力分量（包括三个正应力和六个切应力）。此九个应力分量可写成如下矩阵形式：
应力分量的第一个下标表示作用平面的法向；第二个下标表示应力作用的方向。正应力的两个下标是一样的，故用一个下标简写之。

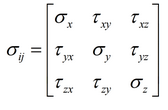
由于切应力互等定理，上列矩阵中对角的切应力是相等的，即：τxy=τyx, τyz=τzy, τzx=τxz。因此，此矩阵为对称矩阵，九个应力分量中六个应力分量是独立的。
主应力

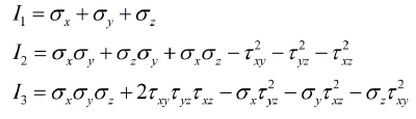
如果作用在某一截面上的全应力和这一截面垂直，即该截面上只有正应力，切应力为零，则这一截面称为主平面，其法线方向称为应力主方向或应力主轴，其上的应力称为主应力。如果三个坐标轴方向都是主方向，则称这一坐标系为主坐标系。
在塑性力学中，常将应力张量分解为：

式中，称为平均正应力。等号右端第一项称为球形应力张量；第二项可记为：

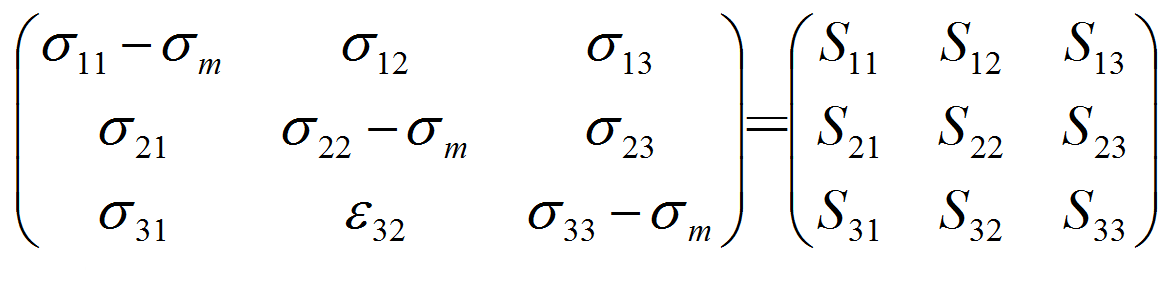
称为应力偏量张量。

 

应力张量不变量
在求解主应力的过程中会得到以主应力为未知数的三次方程，叫做状态方程。

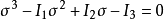
状态方程的三个系数唯一由主应力确定，而一点的主应力是唯一的，这样就得到了不随坐标变化的三个量，叫作应力张量不变量。

 

 

平衡微分方程
以上说明的都是一点的应力状态，而物体内部不同点的应力状态一般是不同的，那么如何描述相邻点间的应力变化关系呢？

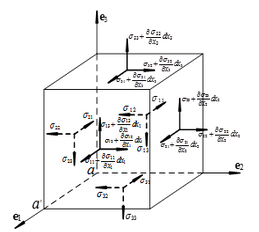
以物体内某一点P(x,y,z)为顶点截取边长分别为dx,dy,dz的直角平行六面体微元，另一个顶点的坐标则为(x+dx,y+dy,z+dz)。根据静力平衡方程，并处理掉高阶小量，得到应力平衡微分方程。